3.3. Statistical Mechanics: Ensembles, Ergodicity and other Stuff#
The physical foundation of simulation is statistical mechanics. Without statistical mechanics, it would be difficult to make the connection between the rather small systems (at most several million particles) simulated for short periods of time with measurements on macroscopic samples. Also most physically important systems are in contact with the rest of the universe, which we call a “heat bath” (although it can be a reservoir for pressure or particles etc.) Statistical mechanics “course grains”- separates the thermodynamic macroscopic variables like pressure and temperature from the microscopic variables: the individual atomic positions and velocities. As we will see the arguments apply also to few body systems in contact with a “bath”.
Even though most of the simulations we will talk about are classical, it is actually easier to understand the fundamental principles if we use the basic concepts of stationary states in quantum mechanics. This is because the energy states (of a finite system) are a countable set while classically position and momentum are continuous variables.
Note
The Phase Space: A classical system is composed of many particles with position, qi, and momentum, pi, denoted as q and p for short. This is the classical phase space. Any conservative mechanical systems can be characterized by a function, H(q, p; t), the Hamiltonian of the system which determines the energy as a function of the coordinates.
Suppose that we have a system with fixed N and V (volume). Then:
There are a finite number of energy levels in any energy range (E, E+dE). We call this the density of states in Phase Space g(E)= exp( S(E) ) where the entropy is S(E).
If we don’t know which state the system is in, the natural assumption is that it is equally likely for the system to be in any of the states in that range. Among the states in this range, all are equally likely. ( A priori equal probabilities is what one assumes for a toss of a fair coin, or for a well-shuffled deck of cards in which each of the 52! arrangements are equally likely.) This was called “principle of insufficient reason” by James Bernoulli (1713) at the start of probability theory, which was furthered by Bayes and Laplace and their non-frequency interpretation of probability. In classical statistical mechanics, the idea of phase space is harder to justify since one has continuous variables; quantum mechanics showed that conjugate variables like position and momentum are the fundamental variable for phase space.
Next consider the interaction between two weakly coupled systems (with Energy E1 and E2 and particle numbers N1 and N2) that are allowed to exchange energy and nothing else. Then for each pair of states, there exists a new combined state with energy E1+E2. This implies that the entropy of the combined system is the sum of the entropy of the two parts. S(E1+E2)= S1(E1)+S2(E2).
If one of the two systems is large (N1 N2 with N1+N2=N), the density of states is enormous and energy will flow to maximize the total entropy. This maximum will occur when the temperatures of the two systems are the same. The temperature (corresponding to the energy E) is defined as 1/T = dS/dE. See notes on entropy and temperature.
The following is the important conclusion of Boltzmann: For a system in contact with a heat bath, \(P(Ei) = exp(-!\beta Ei)/Z\).
Here, \(Z =\sigma_i exp(-\beta Ei)\) is a normalization constant, and is known as the partition function. Usually it is more convenient to work with the (Helmholtz) free energy: \(F = -kT ln(Z)\), since the free energy is proportional to the size of the system, it is an extensive parameter, rather than depending exponentially on the system size. This is also important in computer programs to avoid exponential overflow. All thermodynamic properties can be calculated as various derivatives of the free energy as we will see.
The measured value of some observable (operator \(A\)) will equal the \(Tr(exp(-\beta H) A)/ Tr (exp(-\beta H))\), where Tr=trace or sum of the diagonal elements. This is the quantum version of the more familiar \(< A > = \sigma_i P_i A_i\).
While we have discussed the constant energy ensemble (micro-canonical) we will soon encounter other ensembles, for example, constant pressure, constant temperature (canonical), grand canonical (where the system can exchange particles with the heat bath), etc.
The above discussion was formulated in terms of quantum states. Let us now take the classical limit of the Boltzmann formula. Suppose \(H=K+U\) where K is the kinetic operator and U is the potential operator. For high enough temperatures we can write \(\exp(-\beta H) = \exp(-\beta K) \exp(-\beta U)\). One finds that the probability of being in a volume \(d\vec{p}d\vec{r}\) in phase space is proportional to \(\exp(-\beta E)\) where E is the classical energy \(E= p2/2m+V(R)\). To summarize, if a system is allowed to exchange energy and momentum with outside systems its distribution will equal the canonical distribution. Quantum mechanics does introduce a new feature, an N! coming from the fact the particles are often indistinguishable. Usually but not always, the N! drops out in classical statistical mechanics.
The momentum part of the Maxwell-Boltzmann distribution (the Maxwell distribution) is just a “normal” Gaussian distribution. It is completely uncorrelated with the position part. If you know something about the positions you have no knowledge about the momentum (and vice-versa). The average kinetic energy is exactly (3/2)NkBT (law of equipartition) for a system of N particles, independent of the interactions, unless there are rigid constraints. After doing the momentum integrals, we are left with the configuration distribution and partition function.
3.3.1. Time Average versus Ensemble Average#
In experiments one typically considers a large number of successive times (t1 … tM) to make measurements, each of which reveals the current state of the system. Then = \sigma_i A_iP_i where \(Pi = ni/M\) and ni is the number of times the system is in state i out of M total states. This is a time average over a single system because the values of ni were obtained by successive observations. We will model that by a classical simulation for a fixed number of particles and a given potential energy function V® isolated from any heat bath. Newton tells us the system will evolve according to \(\vec{F} = -\nabla V= m\vec{a}\). We assign initial positions and velocities (implying an initial total energy and momentum). If we let it evolve what will happen? Will it go to the canonical distribution?
First, a few constants of motion maybe be known: energy, momentum, number of particles, etc. These will not change but in a system of more than 2 particles the number of degrees of freedom is greater than the number of constants of motion. Gibbs introduced the artifice of a large number of replicas of the system (i.e., an ensemble) and imagined them to trace out paths on the energy surface. Basically, we could follow A(t) for one system for infinite time and average <Atime>, or just consider the value of A for each member of the ensemble and average<Aens>. Under certain conditions (if the system is ergodic, see Fig. 3.3) one should be the same value. Gibbs adopted the view from the outset that this was only a device to calculate the probable behavior of a system.
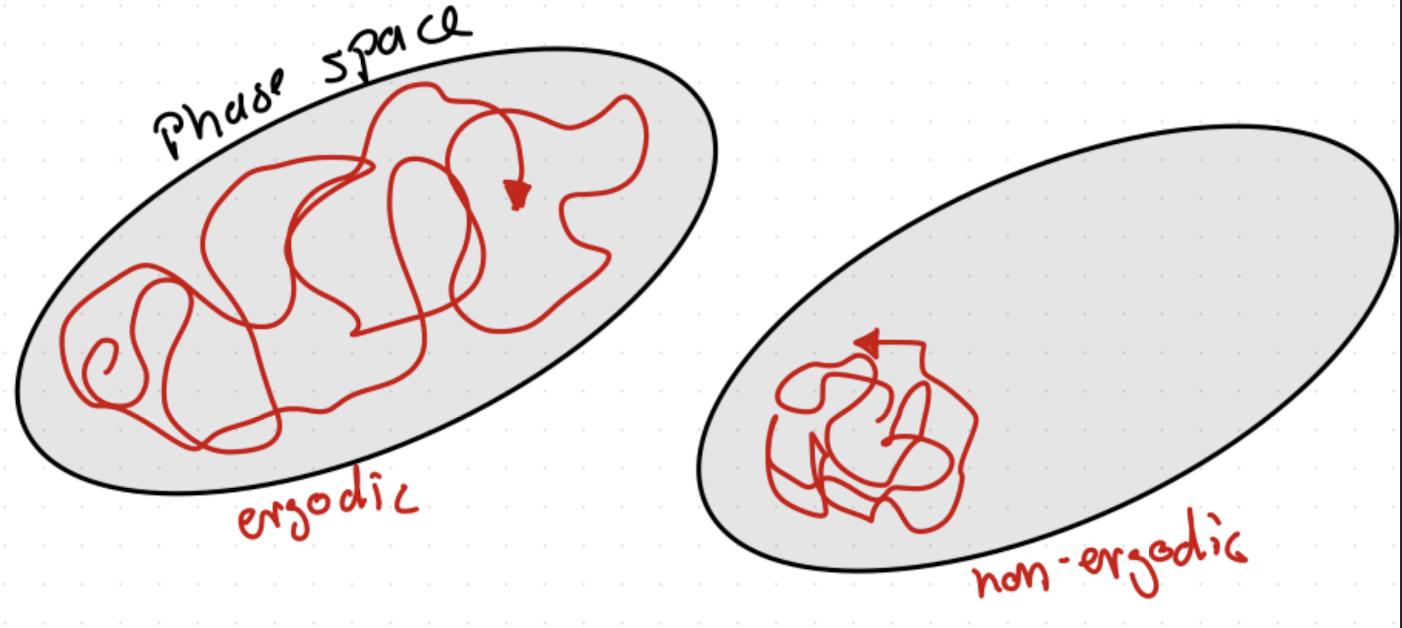
Fig. 3.3 Illustration of phase space with a ergodic and non-ergodic trajectory.#
In other words, instead of starting from a single initial condition, we start from the canonical distribution of positions and momentum. By Louiville Theorem, it is easy to show that this distribution is preserved. What we are doing in Molecular Dynamics, since we do not have the heat bath which gets most physical systems into equilibrium, is to assume that we can interchange the average over initial condition with the average over time. In an MD simulation, tMDsteps cannot go over infinite time, but hopefully an average of long finite tMDsteps is satisfactory. Thus, <Atime>= (1/MDsteps) \sigma_t=1,MDsteps A(t).
Gibbs clearly recognized the relation to entropy to probability and observed the most probable situation (equilibrium) corresponds to maximum entropy subject to given constraints.
3.3.2. The Ergodic Hypothesis#
Is time=ens really true, which is what Boltzmann wanted to prove?
It is true if = <ens>time = <time> ens = time.
Equality one is true if the distribution is stationary.
For equality two, it is assumed that interchanging averages should not matter.
The third equality is only true if system is ERGODIC.
ERGODIC: [adjective] from Greek, erg + hodos (energy path), leading to the German construction “ergodenhypothese” (hypothesis on the path of energy). The Ergodic Hypothesis of Boltzmann (also called the continuity of path by Maxwell) is simply that a phase point for any isolated system passes in succession through every point compatible with the energy of the system before finally returning to its original position in phase space. This journey takes a Poincare cycle.
Ergodicity of a system has been the fundamental assumption of classical statistical mechanics, and it is usually assumed in simulations as well. The assumption (well verified by computer experiments for many but not all systems) is the a path of a million steps or so is a way of sampling the Boltzmann distribution. There are a number of related concepts describing ergodic behavior:
The system, no matter how it is prepared, relaxes on a reasonable time scale towards a statistical equilibrium. The definition of equilibrium is that all macroscopic variables (such as pressure, kinetic energy) are constant in time.
This equilibrium should be characterized by the micro-canonical probability: the integral over the portion of phase space with the given constants of motion. The difference between the micro-canonical distribution and the canonical distribution is order (1/N).
This implies there are no hidden integrals of motion (other than the usual ones-energy, linear and angular momentum, number of particles,…) , and that time correlations decay.
A typical orbit wanders irregularly thoughout the whole energy surface. It will eventually sample all the phase space it can subject to the conserved quantities.
Two orbits, starting out close together are rapidly separated. This is called sensitivity to initial conditions. Typically they diverge exponentially fast with a coefficient know as the Lyapunov exponent.
Actually physical systems and systems being simulated are often not ergodic. They may be either really non-ergodic or non-ergodic in practice (trapped for a time longer than one can simulate).A famous example, one for which scientists are still trying hard to understand is a ?glass?.
3.3.3. Non-Ergodic Behavior#
If the system is non-ergodic; it gets stuck or very slowly decays to equilibrium. This was discovered by Fermi, Pasta and Ulam (FPU) in 1954 on the Los Alamos MANIAC I in perhaps the most profound computer simulation discovery in the early years of computers. These notes are from G. Benettin in MD Simulations of Statistical Mechanical Systems. The FPU Hamiltonian is of N equally massive particles connected by anharmonic springs:
For z = 0, one has decoupled harmonic oscillators with well-known normal modes. For non-zero z, FPU put all the energy into one normal mode and watched the energy spread into the other normal modes. Equipartition says that each mode should get equal energy (at least if you wait long enough). Instead they found:
Let us say here that the results of our computations were, from the beginning, surprising us. Instead of a continuous flow of energy from the first mode to the higher modes, all of the problems show an entirely different behavior. … Instead of a gradual increase of all the higher modes, the energy is exchanged, essentially, among only a certain few. It is, therefore, very hard to observe the rate of “thermalization” or mixing in our problem, and this was the initial purpose of the calculation.
Collected papers of E. Fermi, Vol II, U. of Chicago Press, p 978, 1966.
For higher values of z, the system does approach equipartition after enough time. Thus, whether the system reaches equipartition depended upon its initial conditions. In many respects, this was a precursor to the “chaotic” non-linear dynamics discoveries of the 1980’s.
In the intervening years it has been established that non-ergodic behavior is characteristic of most systems at low enough temperature. It is not a small system or one-dimensional effect, but a low temperature effect. For this reason it is not all that relevant to condensed matter physics since quantum mechanics takes over from classical mechanics at low temperatures. But is something one should be aware of since the temperatures are not all that low. For example, 64 argon atoms below 5K (a good harmonic solid) will never reach equilibrium but stay with whatever phonons they start with. Also celestial mechanics is happy with ordered dynamics. They provide explanations for planetary, ring systems and spiral galaxies.
There are at least 3 different concepts related to ergodicity that characterize a particular system and trajectory:
Integrable system. In these systems the number of constants of motion equal the number of degrees of freedom. They are essentially analytically solvable. A good example is a collection of uncoupled harmonic oscillators. While common in elementary textbooks, they are very rare in nature. Integrable systems can be either periodic or quasiperiodic.
Ergodic trajectory. A trajectory that goes everywhere that is accessible given its constants of motion (such as energy). The KAM theorem states that if an integrable system is subject to a small perturbation the trajectories always stay close to the non-perturbed trajectories and are hence non-ergodic. The FPU system is of this kind. Another good example is the solar system. What is usually meant by ergodic is that the time average over a typical trajectory equals the ensemble average.
Mixing system. Mixing trajectories are sensitive to their initial conditions. Errors (such as contact with a heat bath or numerical errors from the computer precision) grow. In a K-flow system (after Kolmogorov) the perturbed trajectory diverges exponentially in time. The rate is called the Lyapunov exponent. This is the most common situation for many-body systems not at very low temperatures.
On the other hand, in statistical mechanics we expect our system to converge to equilibrium. Whether it does or not cannot usually be proven mathematically but must be determined “experimentally”. In general we don’t know if its ergodic or if it is stuck for a long-time (on our scale). At low temperature very complicated things can happen. It is up to you to decide if it is in fact ergodic. Non-ergodic behavior is both good and bad. On the one hand we are never sure if we have reached true equilibrium (nature has much longer time scales). On the other hand simulation can be used to study metastable states that occur in nature such as the freezing of a super-cooled liquid or a glass. Another example where metastable states may be physically important is in the folding of a protein.
3.3.4. Contact with the outside world#
Often it is good to introduce some contact with a thermal bath. (Langevin equation) Normal laboratory systems are in contact with the outside world. How else can we account for flux of particles, energy and momentum coming from the outside? The boundary conditions depend critically on physics. There is a whole continuum of algorithms that can all sample the same canonical distribution, distinguished from each other by how much randomness is allowed.
Molecular Dynamics (no randomness)
Langevin Dynamics (heat bath adds additional forces)
Brownian Dynamics (heat bath determines velocities)
Forced-bias or Smart Monte Carlo (random walk biased by force)
Classic Metropolis Monte Carlo ( unbiased random walk)
Once one adds any randomness, ergodicity and convergence to the canonical distribution usually follows. Whether any particular run (of finite length) has in fact converged remains an “experimental” question.